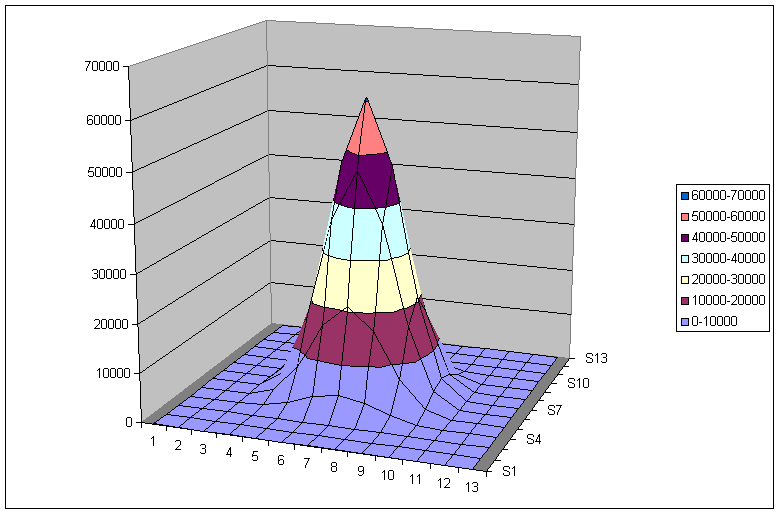
Abb. 1: Die Darstellung unser Test-Gauss-Funktion
Sofort zum vierten Teil (Test-Bilder "Schärfungsmatrix")
Die Methode der "unscharfen Maske"
Das ist hier die Frage! Wie kann man mit einem unscharfen Bild - der unscharfen Maske nämlich - ein Astro-Bild schärfen? Das wollen wir im dritten Teil des Artikels klären.
Die Methode der "unscharfen Maske" wird in der Astro-Fotografie sehr häufig verwendet, um Bilder zu schärfen. Die mathematischen Probleme sind bei diesem Verfahren nicht so groß, wie bei der Schärfungsmatrix. Bei der unscharfen Maske müssen die verschiedenen Matrizen nur addiert und subtrahiert werden.
Wie funktioniert das nun mit der unscharfen Maske?
Ganz einfach. Zunächst berechnen wir vom Astro-Bild ein unscharfes Bild (die unscharfe Maske). Das geht wieder mit einer Matrix-Multiplikation (wie in Teil 1). Nun wird das unscharfe Bild vom Original-Bild abgezogen. Man erhält das sogenannte "Detail-Bild". In diesem Bild sind die Details unseres Astro-Bildes jetzt dargestellt. Nun kommt die letzt Aktion. Man multipliziert jedes Element des Detail-Bildes mit einem Faktor (meistens eine Zahl zwischen ca. 2.0 und ca. 15.0) und addiert das Ergebnis zum Original-Bild. Fertig!
Damit wir genau verstehen, wie das Verfahren rechnerisch abläuft, wollen wir ein Beispiel mit einem Vektor rechnen. Hier ist eine 2-dimensionale Gauss-Funktion eines Sterns. Die bildliche Darstellung sieht man in Abb. 1.
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 256 | 1536 | 3328 | 4352 | 3328 | 1536 | 256 | 0 | 0 |
| 0 | 0 | 1536 | 7168 | 16384 | 20992 | 16384 | 7168 | 1536 | 0 | 0 |
| 0 | 0 | 3328 | 16384 | 36864 | 47360 | 36864 | 16384 | 3328 | 0 | 0 |
| 0 | 0 | 4352 | 20992 | 47360 | 60928 | 47360 | 20992 | 4352 | 0 | 0 |
| 0 | 0 | 3328 | 16384 | 36864 | 47360 | 36864 | 16384 | 3328 | 0 | 0 |
| 0 | 0 | 1536 | 7168 | 16384 | 20992 | 16384 | 7168 | 1536 | 0 | 0 |
| 0 | 0 | 256 | 1536 | 3328 | 4352 | 3328 | 1536 | 256 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |

Abb. 1: Die Darstellung unser Test-Gauss-Funktion
Von unser Zahlenmatrix nehmen wir nun die mittlere Zeile für unsere weiteren Berechnungen (Abb. 2) und erhalten einen eindimensionalen Testdatensatz:
| 0 | 0 | 4352 | 20992 | 47360 | 60928 | 47360 | 20992 | 4352 | 0 | 0 |
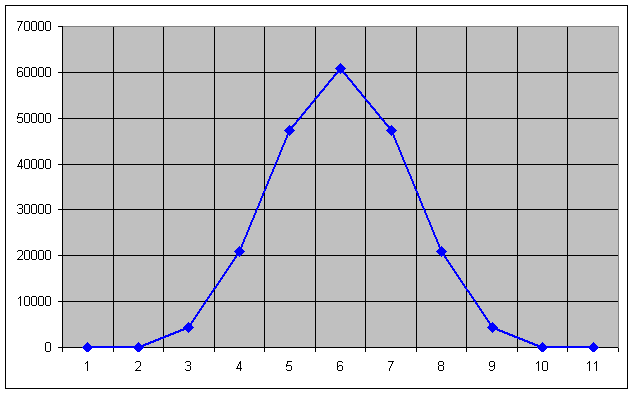
Abb. 2: Die eindimensionale Test-Funktion
Der nächste Schritt ist nun eigentlich der schwierigste von allen. Wir müssen die unscharfe Maske berechnen. D.h., wir müssen von unserem Astro-Bild ein wesentlich unschärferes Bild berechnen. Bisher kenn wir nur ein Verfahren, um Bilder zu schärfen. Das Verfahren, um Bilder unschärfer zu machen, funktioniert aber genauso. Der einzige Unterschied ist in den Elementen der Matrix zu finden. Wir benutzen also keine "Schärfungsmatrix", sondern eine "Unschärfematrix" mit etwas anderen Zahlen. Das Witzige an der ganzen Sache ist nun, das man ein Astro-Bild unschärfer machen kann, indem man es mit einer Matrix multipliziert, die selbst wiederum eine Gauss-Funktion enthält (Gleichung 1).
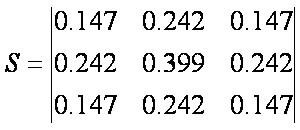
Die Matrix in Gleichung 1 enthält eine gauss-förmige Verteilung. Für unseren eindimensionalen Testdatensatz benötigen wir nur einen Vektor mit einer gauss-förmigen Zahlenanordnung (Gleichung 2).
![]()
Kleiner Einschub: Erstellung einer Matrix mit einer Gauss-Verteilung
Es erhebt sich natürlich noch die Frage, wie man eine Matrix mit diskreten "Zahlenpositionen" mit einer gauss-förmigen Verteilung besetzen kann. Man benutzt Gleichung 3 (aus Teil 1), um die benötigten Werte zu berechnen. Die Matrix stellt dabei das Koordinatensystem dar. Matrixzeilen (waagerecht) sind die X-Koordinate, Matrixreihen (senkrecht) sind die Y-Koordinate. Bei Matrizen mit einer ungeraden Größe (3x3, 5x5, 7x7, usw.) ist das zentrale Matrixelement der "Koordinatenursprung", also X = 0 und Y = 0. Bei Matrizen mit gerader Größe (2x2, 4x4, 6x6, usw.) gibt es kein zentrales Matrixelement. Hier setzt man dagegen den zentralen Punkt zwischen den vier mittleren Matrixelementen auf die Werte X = 0 und Y = 0. Somit haben die die vier mittleren Matrixelemente (um diesen Punkt herum) die Koordinaten: (X = 0.5, Y = 0.5); (X = -0.5, Y = 0.5); (X = 0.5, Y = -0.5) und (X = -0.5, Y = -0.5).
Gleichung 3 aus Teil 1 kann in der vollständigen Form dann folgendermaßen hingeschrieben werden:
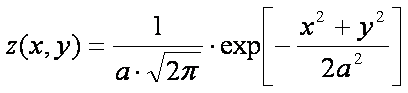
Die obige Gleichung 3 gilt nur dann, wenn man den Koordinatenursprung (Nullpunkt) in die Mitte der Matrix legt (wie oben beschrieben), sonst ist der Bruch im Exponenten etwas komplizierter. Der Parameter a ist für die Breite der Gauss-Verteilung verantwortlich. Je größer der Parameter a ist, desto breiter ist die Gauss-Verteilung. Die Wurzel im ersten Bruch ist eine Konstante und kann vorher ausgerechnet werden. Die Berechnung ergibt: 2.50663.
In einer 5x5-Matrix haben die Matrixelemente dann folgende X- und Y-Koordinaten, welche dann entsprechend in Gleichung 3 bei der Berechnung eingesetzt werden müssen (Gleichung 4):
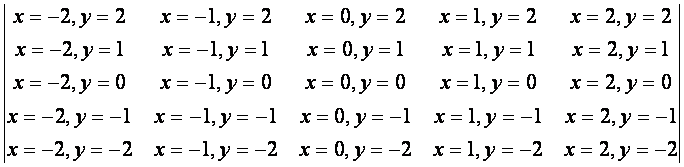
Nun noch eine 4x4-Matrix mit den richtigen Koordinaten (Gleichung 5):
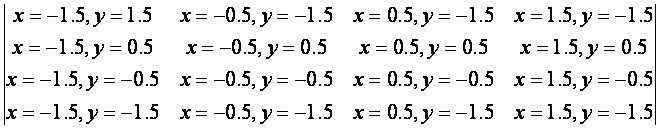
Für andere Matrixgrößen kann man die Koordinatenwerte jetzt sehr leicht mit den beiden obigen Gleichungen ableiten.
Anmerkung: Man kann sich natürlich auch noch andere Matrizen konstruieren, die eine Unschärfe erzeugen.
Und weiter geht's.
Nun müssen wir die Matrix aus Gleichung 2 mit Gleichung 1 multiplizieren, wie wir es in Teil 1 auch mit der Schärfungsmatrix gemacht haben. Die Vorgehensweise ist absolut identisch. Das Ergebnis lautet dann:
| 0 | 1053 | 6817 | 20890 | 38721 | 47233 | 38721 | 20890 | 6817 | 1053 | 0 |
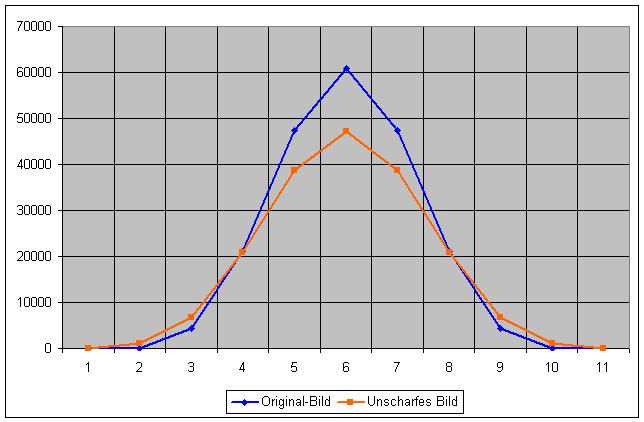
Abb. 3: Die Original-Daten mit den unscharfen Daten
Die neue, orange-farbene Kurve ist etwas niedriger und breiter - also ist diese Abbildung unschärfer als die erste, blaue Gauss-Kurve. Im nächsten Schritt müssen wir nun die orange-farbene Kurve von der blauen Kurve abziehen. Die Subtraktion wird Element für Element durchgeführt:
| 0 | -1053 | -2465 | 102 | 8639 | 13695 | 8639 | 102 | -2465 | -1053 | 0 |
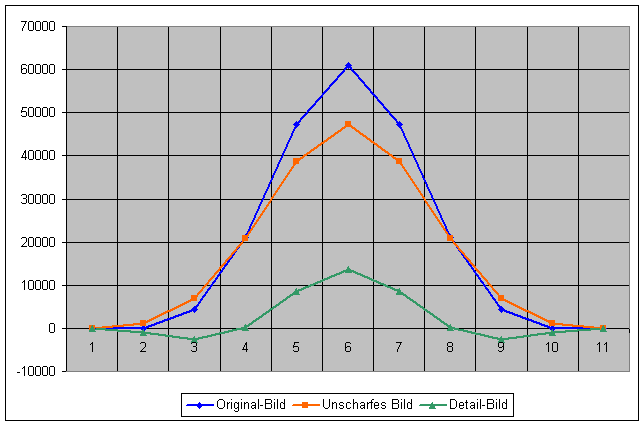
Abb. 4: Das Detail-Bild
Das neue Bild nach der Subtraktion (grüne Kurve) wird häufig auch "Detail-Bild" genannt. In dieser Kurve finden wir auch wieder einige negative Werte. Das erinnert uns an die Berechungen mit der Schärfungsmatrix (Teil 1). Auch hier traten negative Werte auf. Im letzten Schritt wird nun ein Vielfaches des Detail-Bildes zum Original-Bild hinzuaddiert. In diesem Fall wollen wir das 5-fache Detail-Bild zum Original addieren. Es wird jedes einzelne Element der Detail-Kurve mit dem Faktor multipliziert und dann zum entsprechenden Element der Original-Kurve addiert:
| 0 | -5265 | -7973 | 21502 | 90555 | 129403 | 90555 | 21502 | -7973 | -5265 | 0 |
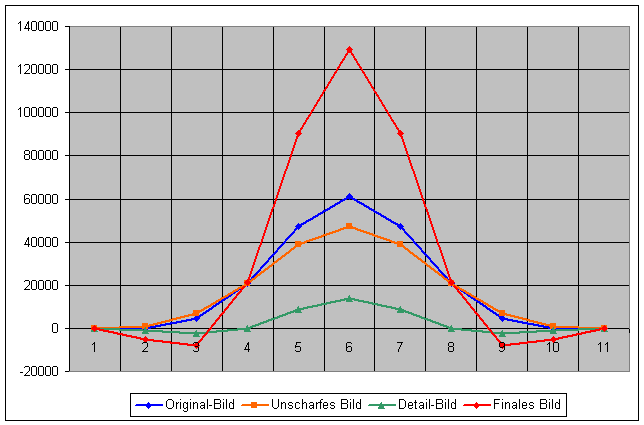
Abb. 5: Die rote Kurve zeigt das (fast) endgültige Ergebnis
Das "fast" fertige Ergebnis ist in Abb. 5 zu sehen. Nun muss man nur noch die negativen Werte, die man ja auch einem Bildschirm nicht darstellen kann, durch den Wert "0" (oder durch das Hintergrundrauschen des Astro-Bildes) ersetzen:
| 0 | 0 | 0 | 21502 | 90555 | 129403 | 90555 | 21502 | 0 | 0 | 0 |
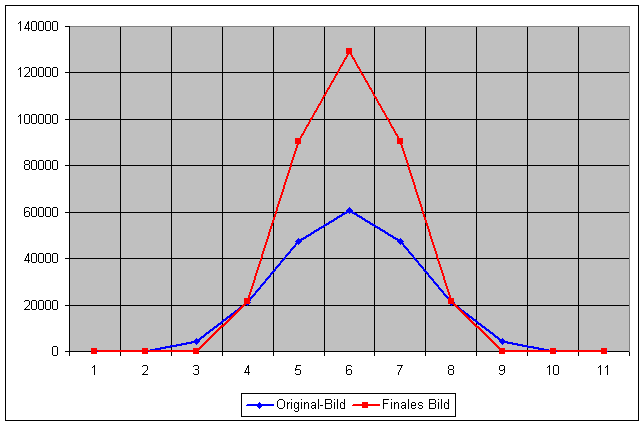
Abb. 6: Die endgültig fertige berechnete Kurve
Wenn man die Original-Kurve (blau) und die neu berechnete, geschärfte Kurve (rot) in Abb. 6 betrachtet, erkennt man, dass die Schärfung durch eine Abschwächung der Werte im unteren, nicht so intensiven Bereich und durch eine Verstärkung im intensiven, mittleren Bereich erzielt wird. Der gleiche Algorithmus kann nun natürlich auch auf 2-dimensionale Gauss-Funktionen mit der entsprechenden Wirkung angewendet werden. Abb. 7 zeigt die vollständige Anwendung des vorgestellten Rechenalgorithmus auf die 2-dimensionale Gauss-Funktion aus Abb. 1.
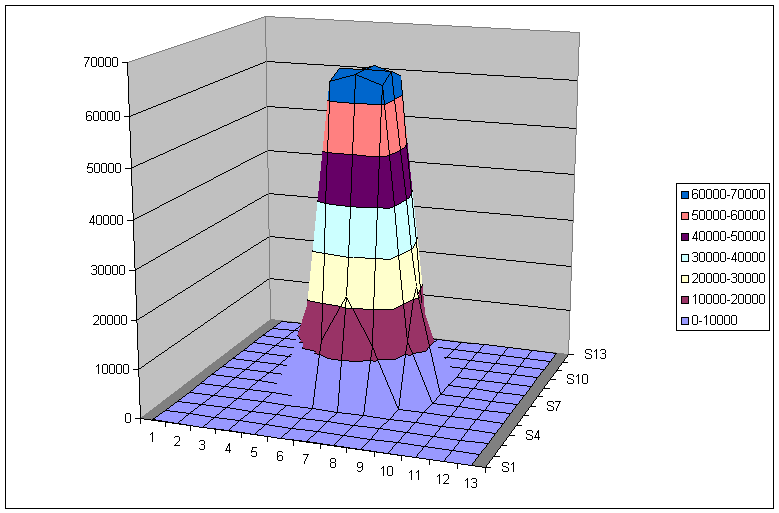
Abb. 7: Das Ergebnis der "unscharfen Maske" mit einer
2-dinmensionalen Gauss-Funktion
Allgemein kann der Algorithmus für die "unscharfe Maske" folgendermaßen dargestellt werden:
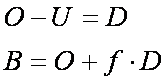
O = Original-Bild
U = Unscharfes Bild
D = Detail-Bild
B = Endgültiges Bild
f = Faktor für Detail-Bild
Bei dem Verfahren mit der unscharfen Maske haben wir zwei Parameter, die wir modifizieren können, um einen anderen Schärfungsgrad zu erzielen. Zum einen kann man ein mehr oder weniger unscharfes Bild erzeugen, indem man die Gauss-Funktion der Matrix S (Gleichung 1), die vom Original-Bild abgezogen wird, "flacher" oder "steiler" errechnet. D.h., der Sigma-Wert der Gauss-Funktion (siehe Teil 1) wird größer oder kleiner angegeben. Andererseits kann man den Faktor variieren, mit dem das Detail-Bild multipliziert wird, bevor es schließlich zum Original-Bild addiert wird. Das macht das Ganze natürlich wieder etwas schwieriger und unübersichtlicher. Aus diesem Grund müssen natürlich viele reale Test-Bilder berechnet werden, um den Algorithmus zu beurteilen. Diese sind im vierten Teil des Artikels dargestellt.
Weiter zum vierten Teil (Test-Bilder "Unscharfe Maske")
Zurück zum zweiten Teil (Test-Bilder "Schärfungsmatrix")